A Primer on Arabic Numeral Harmonic Analysis in Modern Modal Music
Alexander LaFollett
If you have encountered my theoretical work on the area of modal and non-tertian harmony, such as my exploration of harmonic syntax in the Locrian mode, you would have also run across my Arabic numeral analysis system, which I use to label chords in this harmonic environment. While that particular writing does explain some of the concepts underlying this form of analysis, I feel that an essay specifically dedicated to this topic is warranted here.
What is Arabic numeral harmonic analysis, and why is it necessary?
Arabic numeral harmonic analysis is a method of analyzing and labeling chords, comprising a wide array of interval structures, and describing how they fit within the context of a prevailing modal structure. It is an approach I have been developing since 2005, when I needed new tools to analyze my orchestral pieces Hydrogen and Helium, from my master’s thesis (finished 2006).
The underlying concept is very similar to Roman numeral analysis, but was designed to overcome some of the deficiencies that one quickly encounters when analyzing modal and non-tertian harmony using that approach. It even addresses some of the issues one encounters using Roman numerals for their original purpose of analyzing tonal harmony, which is arguably nothing more than a restrictive subset within the broader field of modality. Because of this similarity to one of the most familiar concepts in music theory—one that occupies a considerable amount of time in the traditional two-year post-secondary theory curriculum—it also becomes very easy to grasp.
The Arabic numeral system also allows one to at least begin to address a matter in the analysis of modal music that I feel has been largely ignored to date—that being the matter of how the sense of mode is being established, and at an even deeper level, how the harmonies and the individual scale degrees behave within the context of the mode.
Much of the analysis to date in the area of modality has been occupied with surface-level details—often just identifying the mere fact that there is a mode in use, and what to call it, since the matter of nomenclature is haphazard and severely underdeveloped in current general usage, especially once one gets outside the familiar realm of the diatonic modes. The “battle royale” between Pieter van den Toorn, Dmitri Tymoczko, and Daniel Chua (the latter of whom called the whole matter a “riot”, fittingly enough) over the mere labeling of the modality at the opening of the “Augurs of Spring” section from Stravinsky’s The Rite of Spring is just one symptom of this. The fact that much of the general educational instruction on modality, a considerable amount of which is contained in non-academic method books, is little more than “here’s some scales (some of which are actually the same scale but with different names—a particular hallmark of some recent method books), go figure it out on your own” is another.
The general apparatus for handling non-tertian harmony—chords built out of intervals other than thirds—is also arguably quite underdeveloped, particularly in dealing with it from the perspective of its use in harmonic progressions in a centric environment (i.e. both modality and common practice tonality), not as merely an abstract collection of intervals, or as some sort of “nonfunctional” fluff that can be ignored.
The matter of behavior and harmonic syntax is also a rather critical matter for composers and songwriters wishing to explore modality and non-tertian harmony, and I have often been asked about it by students, as well as in general conversation with other musicians, as it really isn’t discussed beyond a cursory level. As someone who sees himself as a composer-theorist—with an emphasis on the dash, as in contrast to recent trends, the two sides are virtually inseparable for me—this is a matter I find particularly important.
How does it operate?
The basic syntax for the Arabic numeral labels follows the format b(spec), where the b is the Arabic numeral (i.e. 1, 2, 3, etc.) that represents which scale degree from the mode is in the bass—similar to Roman numerals—and spec is the species of chord that is built upon it. The species is defined as the interval structure built on top of that bass degree, generally condensed down to the span of an octave (i.e. simple intervals), and put in order of smallest to largest interval above the bass—such that 7 is the largest number seen in the species designation.
If, for instance, we consider the example of the chord D-G-C in the context of A Aeolian (A-B-C-D-E-F-G-A), D is scale degree 4. The G lies a fourth above D, and the C a seventh above, meaning that the species of the chord is 4/7, and the full label would be a 4(4/7).
For another example, let us consider the chord E-G♯-B-D-F♯ in the context of E Mixolydian (E-F♯-G♯-A-B-C-D-E), E is degree 1. G♯ is a third above, B a fifth, and D is a seventh above. The F♯ lies above the seventh in the voicing of the chord, and if we subtract the octave out of the resultant ninth, we are left with a second. Putting this into order, the chord would accordingly be labeled as a 1(2/3/5/7).
Structures that contain the same octave-condensed relationship to the bass, regardless of the ordering, voicing, or doubling of those non-bass notes, will all belong to the same species. All of the following chords, for instance, would be classed as 3/5 chords.
All have C in the bass, and also have an E (a third above, or some octave multiple thereof) and a G (a fifth above, or again some octave multiple thereof) present. C-E-G, C-G-E, and C-G-E-C (canceling out the duplicate C) would all reduce down to C-E-G. (Orderings of these three notes in which C is NOT in the bass, however, like E-G-C or G-C-E, are not 3/5 chords, a matter described in more detail later.)
There are actually a total of 64 (!) different species possible within a heptatonic mode, counting the trivial “singleton” (literally just a single note, wherein no species designation would be shown in the Arabic numeral label), and the catch-all “heptachord” or “full modal aggregate”—designated as 2/3/4/5/6/7—in which all notes of the mode are present above the bass.
This effectively means that, excluding the trivial singletons, each mode has a total of 441 possible native chord structures—63 over each of the seven scale degrees.
How does this system handle chord qualities?
With respect to the matter of chord qualities, the typical application of the Roman numeral system uses upper and lower case (for “major” (IV) and “minor” (iv), respectively), along with three common modification symbols, to handle the “augmented” (+), “diminished/fully-diminished” (°), and “half-diminished” (ø) cases. Occasionally, some special situations (i.e. augmented sixth chords and altered dominants) may bring about a bit of additional symbology, but there’s not much else needed. The majority of this, however, is done within the context of a two-mode system, with a very limited set of the above species being considered—primarily just 3/5, 3/5/7, and their rotations (“inversions” in the common practice tonal nomenclature).
Once one begins to accept the idea of additional modal and species possibilities, a wider array of qualities also becomes possible, and the options presented by the traditional Roman numeral quality symbology are either quickly exhausted, or start to seem questionable to use. Even a structure as simple as the 4/5 chord D-G-A poses such a dilemma—the two intervals above the bass are classed as “perfect” under the traditional nomenclature. The fact that the Arabic numerals don’t have typographical cases in the same way as Roman numerals also factors into the equation.
The most natural and concise solution I have found is to use the modes themselves as quality identifiers, essentially as an extension of “chord-scale theory”. This bears some resemblance to how things are typically handled in the jazz idiom, though excising the vestigial remnants of common practice tonality that regularly figure into the nomenclature there. To give a familiar example, I will first examine the case of 3/5 chords.
The system that I have derived involves labeling the qualities based on the first mode in my Heptatonic Modal Catalog that contains that particular quality on degree 1. The ordering I use in the catalog for the diatonic series begins with Dorian as Mode 1 (due to historical precedent, and the fact that the mode has some rather unique properties, like its underlying palindromic structure), Phrygian as Mode 2, and so on, ending with Ionian as Mode 7.
If we build 3/5 chords on degree 1 of each of these modes, we find the following:
| MODE | SCALE | Deg 1 | Deg 3 | Deg 5 | First Time for Interval Pattern? |
|---|---|---|---|---|---|
|
1 – Dorian |
D-E-F-G-A-B-C-D |
D |
F (3H) |
A (7H) |
Yes |
|
2 – Phrygian |
E-F-G-A-B-C-D-E |
E |
G (3H) |
B (7H) |
No, same as Dorian |
|
3 – Lydian |
F-G-A-B-C-D-E-F |
F |
A (4H) |
C (7H) |
Yes |
|
4 – Mixolydian |
G-A-B-C-D-E-F-G |
G |
B (4H) |
D (7H) |
No, same as Lydian |
|
5 – Aeolian |
A-B-C-D-E-F-G-A |
A |
C (3H) |
E (7H) |
No, same as Dorian |
|
6 – Locrian |
B-C-D-E-F-G-A-B |
B |
D (3H) |
F (6H) |
Yes |
|
7 – Ionian |
C-D-E-F-G-A-B-C |
C |
E (4H) |
G (7H) |
No, same as Lydian |
Dorian, Phrygian, and Aeolian all have the 3-half-step third, and 7 half-step fifth; Lydian, Mixolydian, and Ionian all have a 4-half-step third and 7-half-step fifth, while Locrian has a 3-half-step third and a 6-half-step fifth. The 3H/7H quality, given that it first arises in Dorian (Mode 1), becomes the Dorian 3/5 chord. Lydian (Mode 3) is the first to have the 4H/7H species, which thus becomes the Lydian 3/5. The 3H/6H model, accordingly, becomes the Locrian 3/5. Coincidentally enough, this Dorian/Lydian labeling ends up producing a more transparent reading of the common jazz theory chord-scale models.
In order to better show off the real benefits of this system, I will now provide an example featuring a less familiar species—the 2/5/6 chords. Following the same process as above for the diatonic modes, we get the following results:
| MODE | SCALE | Deg 1 | Deg 2 | Deg 5 | Deg 6 | First Time for Interval Pattern? |
|---|---|---|---|---|---|---|
|
1 – Dorian |
D-E-F-G-A-B-C-D |
D |
E (2H) |
A (7H) |
B (9H) |
Yes |
|
2 – Phrygian |
E-F-G-A-B-C-D-E |
E |
F (1H) |
B (7H) |
C (8H) |
Yes |
|
3 – Lydian |
F-G-A-B-C-D-E-F |
F |
G (2H) |
C (7H) |
D (9H) |
No, same as Dorian |
|
4 – Mixolydian |
G-A-B-C-D-E-F-G |
G |
A (2H) |
D (7H) |
E (9H) |
No, same as Dorian |
|
5 – Aeolian |
A-B-C-D-E-F-G-A |
A |
B (2H) |
E (7H) |
F (8H) |
Yes |
|
6 – Locrian |
B-C-D-E-F-G-A-B |
B |
C (1H) |
F (6H) |
G (8H) |
Yes |
|
7 – Ionian |
C-D-E-F-G-A-B-C |
C |
D (2H) |
G (7H) |
A (9H) |
No, same as Dorian |
The resultant four species, per the above example, would be the Dorian 2/5/6 (2H/7H/9H), the Phrygian 2/5/6 (1H/7H/8H), the Aeolian 2/5/6 (2H/7H/8H), and the Locrian 2/5/6 (1H/6H/8H).
The interesting thing about doing this quality analysis is that it yields knowledge about the relationships between scale degree positions between modes, which might not otherwise be initially considered—especially due to the way in which the ubiquity of common practice tonal ideas has conditioned many Western musicians to think on a tertian basis when dealing with music that has tonal center. This sort of knowledge is, I believe, of particular utility for those writing music that makes use of modality and/or non-tertian harmony.
Expanding out to the full breadth of all 462 heptatonic modes that are possible within the space of 12-tone equal-temperament (12-TET)—which also comprises the full extent of the Heptatonic Modal Catalog—there are actually a total of twenty-one different qualities available for just the 3/5 chords alone. In fact, each of the fifteen possible 3/5 species have twenty-one qualities apiece. The lone heptachord species—2/3/4/5/6/7 (under which the tertian construct of the “thirteenth chord” would be encompassed)—actually contains a total of 462 qualities, just as many as there are modes.
These sheer numbers may seem daunting, though unless one ventures into the wilds of highly-eccentric heptatonic modes (think B♯-C♯-D-E♭-F♭-G♯-A♯-B♯), one will likely only encounter a more manageable subset of all of these possibilities. That said, the biggest thing that the presence of all these species, qualities, and modes bring to the table is a heightened ability to control musical expression, and one that starts from a familiar base.
Another interesting fact to note is that the alteration of a single note in a mode—i.e. changing C Ionian into C Mixolydian by lowering scale degree 7—will result in 255 harmonic structures within the mode (out of 441—about 57.8%) changing qualities. That is a statistically significant figure.
How does this system handle the concept of inversions?
Simply put, it doesn’t.
That may seem like a shocking statement, and an admission of what one would initially imagine to be a gaping hole in the system. However, there are a number of significant logical, musical, and historical inconsistencies with the concept, at least as it is usually thought of in established tonal theory. As such, its exclusion is very much by design. The nature of working in a modal harmonic environment, in which both non-tertian harmony and seemingly warped forms of tertian harmony are common, often magnifies these inconsistencies to an extreme, causing the entire concept to break down with considerable frequency.
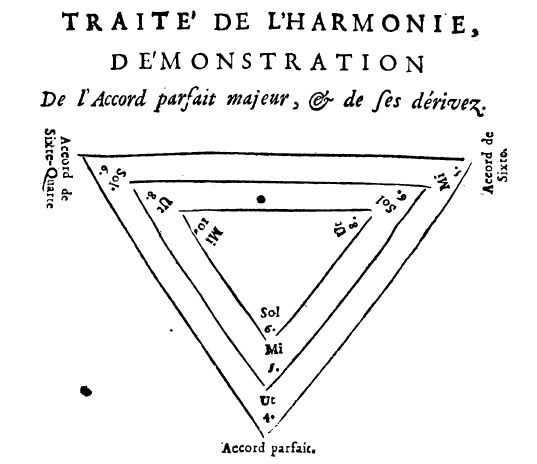
To review the basic premise as is traditionally taught in tonal theory, the notion is that the chords C-E-G, E-G-C, and G-C-E, by virtue of containing the same notes (C, E, and G), are all effectively the same chord, “C Major”, and have the same root—C—despite the fact that the latter two have a different note in the bass. Because of the “non-root” bass in the latter two, they are considered to be “first inversion” and “second inversion” of the former, which is in “root position”. This notion is based on the idea of tertian primacy, and Jean-Philippe Rameau popularized the idea of tying it all to the overtone series in his Traite de l’harmonie (“Treatise on Harmony”) in 1722, using the fact that the inversions of the major triad (or Lydian 3/5) can be derived from higher partials off the fundamental of the apparent root, as shown in his well-known “triangle diagram”:
Technically, my approach with inversion is to replace the concept with a new related one, which happens to be derived from an already integral part of modal theory—rotation. If we examine the basic process used in common practice chord inversion with a triad, for example, C-E-G, we find that the first step moves the root (C), up to the top of the structure, making E be the lowest note—E-G-C. Following this process again, the E gets moved up to the top, leaving the G at the bottom.
This is, of course, parallel to the relationship between the different modes. Taking the unique pitches of D Dorian, ignoring the usually included octave repeat (D-E-F-G-A-B-C), and moving them around such that the first pitch, D, gets moved to the back of the order, with the other pitches moving forward, the result is E-F-G-A-B-C-D. This result is E Phrygian—centered on E, not on D. If we stack D Dorian up in thirds, to create the traditional concept of a thirteenth chord, as D-F-A-C-E-G-B, the result of an “inversion” is F-A-C-E-G-B-D—yet another thirteenth chord, which corresponds to F Lydian (F-G-A-B-C-D-E-F) stacked in thirds. Again, this structure is centered on F, not on D.
Beyond this, there is the fact that Rameau himself was not consistent with the concepts he set up in 1722. Under the paradigm from Traite de l’harmonie, the chord C-E-G-A would be regarded as the first inversion of the seventh chord A-C-E-G, with A as the root. However, in one of his later treatises, Génération harmonique from 1737, Rameau begins theorizing about the concept of a sixte ajoutée, or “added sixth chord”, and possibility that the structure C-E-G-A might actually be rooted on C after all, at least in certain situations. There’s also the matter that some more recent tonal theorists—especially those of a Schenkerian bent—have been regularly questioning the concept in various fashions, primarily with second-inversion triads, as evidenced by David Beach (1967), as well as noted theory textbook authors Edward Aldwell and Carl Schachter. Despite Rameau’s later reconsideration—and the fact that the sixte ajoutée has found favor in jazz and popular idioms—the earlier, uncorrected version of his theory is still almost taught as gospel in the traditional, classically-oriented theory coursework.
And this does not even begin to touch the matter of non-tertian chords. The most notable attempt to apply this same sort of inversion logic to non-tertian harmonies came from Paul Hindemith, in his 1937 treatise, The Craft of Musical Composition. His rationale is based on difference tones—by-product tones produced by the frequency difference between two other pitches—generating theoretical non-bass “roots” for certain structures (or in some cases, rendering them “rootless”). William Thomson, however, riddles Hindemith’s theory with holes in his 1993 Music Perception article “The Harmonic Root: A Fragile Marriage of Concept and Precept”, for its impracticality and imperceptibility.
How does this modal idiom handle the case of 3/5 chords, then? Following mode rotation logic with C-E-G, this would imply that C-E-G, E-G-C, and G-C-E are all “modes”, so to speak, of the same series, produced through the same rotation process. The first would have C as its “center”, the second E, and the third G, rather than all being rooted on C.
If we are in the context of C Ionian, the Arabic numeral symbols would be 1(3/5), 3(3/6), and 5(4/6), respectively.
In this situation, the supposed “root weakness” of the latter two chords, rather than being explained by Rameau’s original inversion theory from 1722 (which he himself started to contradict 15 years later), is instead explained by a concept I refer to as solidity. The idea of solidity, which loosely takes inspiration from the perception research of Richard Parncutt (1988) (and by extension, the earlier work of Ernst Terhardt (1979)), posits the notion that various intervals have different tendencies to strengthen or weaken the gravity projected by the bass note.
My theory of solidity currently is two-pronged, with hierarchies based on both generic intervals (i.e. seconds, thirds, etc.) and specific intervals (in half-steps), which provides the system more nuance in handling extended modal contexts, where positioning on both continua is important. With respect to generic intervals, the hierarchy, from most “solid” to least, goes as follows: fifths, thirds, sevenths, seconds, fourths, and finally, sixths. The first two are strongly solid, the second two are moderately so, and the latter two are not particularly solid at all. Accordingly, at this general level (which is true for the diatonic modes), 3/5 is an incredibly solid structure at the general level, while 3/6 and 4/6 are particularly weak and ineffective in establishing a tonal center in a modal context at this same level. The solidity approach helps provide a more logically consistent explanation of these chords, and of some phenomena in Renaissance counterpoint, such as the curious treatment of the perfect fourth.
How does this system handle altered chords?
In cases where notes have been altered from those present in the mode, my solution is to simply use plus (+) and minus (-) symbols, showing the direction of the alteration—this allows for the unambiguous identification of the alteration. In the context of using the chord E-G♯-A in D Dorian (D-E-F-G-A-B-C-D), one would first see that E is degree 2, and—ignoring the accidentals/inflections following the upper pitches—that G(♯) and A are a third and fourth above, resulting in a species designation of 3/4. The 2(3/4) chord native to D Dorian would be E-G-A, so comparing this to E-G♯-A, we see that the third of the chord has been raised by 1H, giving us a symbol of 2(+3/4).
Staying with D Dorian, if one were to encounter the chord B♭-D-F, one would see that the root, B♭, does not exist in the mode, but can be produced by lowering degree 6 (B) by 1H. The other two notes in the chord, D and F, do exist in the mode, and therefore, are not altered. The resultant symbol would be -6(3/5).
In the case of a situation where there is pervasive mixture of two forms of a scale degree—something I term a polymodal complex, where no single component mode from the complex can be clearly identified as the prevailing mode (and thus, no way of definitively determining which option is native to the mode, and which is an altered degree), then it may become useful to mark these different forms by using up (↑) and down (↓) arrows to prefix instances of these different options for this degree. One of the most applicable cases would actually be with “minor” in a common practice context—which, if all the supposed “forms” are merged together, can very easily be described as such a polymodal complex , in which degrees 6 and 7 have upper and lower options (i.e. A-B-C-D-E-[F-F♯]-[G-G♯]-A, where either F or F♯ can be used for degree 6, and either G or G♯ for degree 7). The familiar “vii°” from Roman numeral reckoning in this context would be rendered as ↑7(3/5) (and be of Locrian quality), while the subtonic “VII” would be ↓7(3/5) (and be of Lydian quality).
What does this mean with respect to the notion of “non-chord tones”, and harmonic salience?
In the comfortable confines of common practice tonality, the notion that “if it doesn’t fit in a stack of thirds, it’s probably not a chord tone” makes things virtually automatic in many situations. As soon as one drops the assertion of tertian primacy embedded in tonal theory, however, things start to become much more subjective—and much more complicated. With all of these chord species now existing as valid entities, theoretically, one could actually dispatch with the idea of non-chord tones altogether, and analyze every single vertical pitch structure in a piece of music using this system. (For the record, I have actually done this, with two of my orchestral pieces, no less. The full harmonic breakdown ended up taking the form of a spreadsheet.)
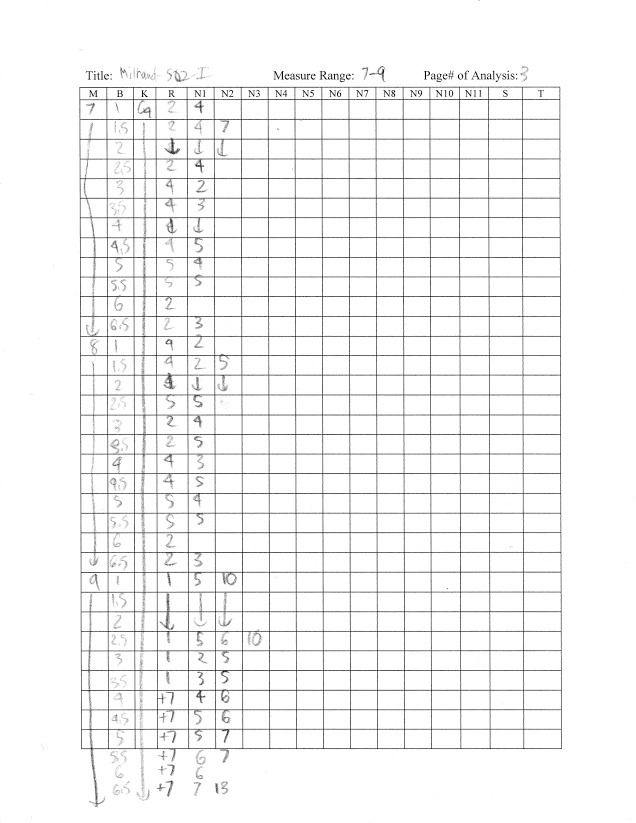
I also attempted to do this note-by-note spreadsheet analysis with Darius Milhaud’s String Quartet No. 2. (Note this is with an early prototype of the Arabic numeral system.)
This, however, raises the questions as to whether or not this is advisable, and to what extent certain chords/vertical pitch structures can be considered “structural” or “salient” in the music. If one were to try to assign priority of some chordal structure over a given duration, it would likely revolve around features such as:
(a) harmonic rhythm and the durations associated with the various pitches (i.e. pitches/structures that are sustained longer, and those that land at regular and/or metrically stronger points), as well as the frequency of their appearance and register.
(b) the nature of the prevailing musical texture and its activity levels (i.e. whether one is dealing with a chorale, a drone-accompanied melodic line, or a fugue).
(c) the types of harmonic structures that seem to be most prevalent—effectively “pattern-matching”, akin to the “stack of thirds” rule from tonality, but with more flexibility in determining what the pattern can be—for instance, a stack of sevenths.
(d) any sort of arpeggiation or chord outlining within the musical lines.
Taking these sorts of features into consideration can lead one to perhaps come up with some sort of generalized reduction, perhaps bearing some superficial resemblance to Schenkerian analysis (though used in a way that Heinrich Schenker himself certainly would not have approved, given his anti-modal sentiments), which could then be used to hone the targets of an Arabic numeral harmonic analysis to the most essential pitches.
On the opposite end of the spectrum—should there be some reason to zoom in on a particular harmonic happening in a segment of music, minus certain factors, to pick up some finer detail that would perhaps go unnoticed otherwise, the prospect of doing so is also viable.
Ultimately, analysis often becomes a highly subjective matter, and this is especially true once one begins to deal with techniques such as these on complex pieces of music. That is, for me personally, one of the great joys of it—the fact that there often is no single “right answer”, and the fact that music theory, in many ways, is the art of creating some form of scientific logic about a piece of art, which requires both rational and creative thinking.
Alexander LaFollett, Ph. D.
16 December 2019
REFERENCES
Aldwell, Edward, Carl Schachter, and Alan Cadwallader. 2018. Harmony and Voice Leading, 5th ed. Boston, MA: Cengage Learning.
Beach, David. 1967. “The Functions of the Six-Four Chord in Tonal Music.” Journal of Music Theory 11/1, 2-31.
Chua, Daniel K.L. 2007. “Rioting with Stravinsky: A Particular Analysis of The Rite of Spring.” Music Analysis 26, 59-109.
Hindemith, Paul. 1937 [1945]. The Craft of Musical Composition, translated by Arthur Mendel. London: Schott.
LaFollett, Alexander. 2006. “Analysis of Hydrogen and Helium for Large Orchestra.” Master’s thesis, Central Washington University.
LaFollett, Alexander. 2019. Heptatonic Modal Catalog, 2019 edition. Forest Grove, OR: Sonata Enterprises.
Parncutt, Richard. 1988. “Revision of Terhardt’s Psychoacoustical Model of the Root(s) of a Musical Chord.” Music Perception 6.1, 65-93.
Rameau, Jean-Philippe. 1722. Traite de l’harmonie. Paris: J.B.C. Ballard.
Rameau, Jean-Philippe. 1737. Generation harmonique. Paris: Prault.
Terhardt, Ernst. 1979. “Calculating virtual pitch.” Hearing Research 1, 155-182.
Thomson, William. 1993. “The Harmonic Root: A Fragile Marriage of Concept and Precept.”Music Perception 10.4, 385-415.
Tymoczko, Dmitri. 2002. “Stravinsky and the Octatonic: A Reconsideration.” Music Theory Spectrum 24, 88-102.
van den Toorn, Pieter and Dmitri Tymoczko. 2003. “Stravinsky and the Octatonic: The Sounds of Stravinsky.” Music Theory Spectrum 25, 167-202.











1 pings
[…] A Primer on Arabic Numeral Harmonic Analysis in Modern Modal Music […]