ABOUT MODES: FOR THE THEORETICALLY CURIOUS
What is heptatonic modality?
Heptatonic modes are essentially pitch spaces that consist of seven distinct pitch classes within the range of one octave. Some of the most familiar pitch materials in Western music (and many world musics for that matter) are technically heptatonic modes, including the familiar “major” and “minor” scales and the “church modes” (i.e. Dorian, Phrygian, etc.). The category also extends to include a number of less familiar (and much less familiar) modes, which form the basis of my “system”.
Why heptatonic modality?
There are a number of features that attracted me to taking a modal approach. My own entry into it came about as a result of my outgrowing “traditional” tonality in the early 2000s. Even very early in my musical training, there were certain fundamental aspects of tonal music that never really appealed to my ear, including the “Major Scale” (Ionian mode) itself. I began to alter, re-appropriate or relocate the leading tones that often drive tonal music forward as part of the tonic-dominant relationship, and that led me toward something that more resembled modality. I began appropriating other modal forms into my music shortly thereafter. This was mainly upon realizing that I had already been making some consistent “chromatic warping” to diatonic modes (creating de facto “paradiatonic” modes, which aren’t strictly “diatonic” but behave similarly), and that the augmented triad did not exist natively within the rubric of the church modes.
Staying within a heptatonic framework still allowed me to appropriate a musical language that could still bear some resemblance to tonality, while sounding different and fresh. I have also had a certain attraction to asymmetry in my music. Rather than the drive toward “symmetry as perfection” oft-cited in discussions about many modernist composers of the 20th century, my approach is more about “asymmetry begetting infinity”. Indeed, there is a larger array of unique collections of seven pitch classes than collections of any other size within 12-tone equal temperament (12-TET) tuning.
How many modes have you catalogued?
There are 462 heptatonic modes in my system, all existing in 12-TET space, laid out in 66 “series”, each consisting of 7 rotationally-related modes. Because there are no “modes of limited transposition” included, each of these modes can be transposed 12 times, creating the equivalent of 5,544 “key areas”. Going along with the tradition of the more familiar modes, they have all been given names relating to ancient (predominantly Greco-Roman) geography. This serves to give the modes a bit more memorable identity and character, and to provide a unified identity for a few popular “paradiatonic” (non-church mode) formations that have accrued as many as a dozen names in the literature, or have only been referred to by impersonal catalog numbers.
What do these things look like?
Here’s a few that I use somewhat regularly:
MODE 38—SKYRIAN

MODE 12—DARDANIAN

MODE 16—ANDRIAN

MODE 187—THASIAN

MODE 241—ILIAN

MODE 188—DACIAN

MODE 67—SPARTAN
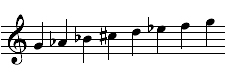
MODE 359—ZACYNTHIAN

Where do the names originate?
Like the original “church modes”, the names reference ancient geography, primarily of Greco-Roman origin. The names help impart the sense that the modes are all part of the same continuum, on equal footing with the familiar modes, and also help clear up the extremely confusing and non-standardized nomenclature for paradiatonic modes, whereby many modes have been given no real name, whereas others have acquired dozens in the literature.
For example, let’s consider Mode No. 14. If you’re at all familiar with so-called “synthetic scales”, you’ll recognize it instantly.
MODE 14

But in the existing theoretical literature that I’ve seen, Mode 14 is called by at least 11 different names: Lydian-Dominant, Lydian-Mixolydian, Lixian, Lydimixolydian, #4 b7, Lydian b7, Mixolydian #4, Bartok, the “Howard Hanson Symphony No. 4 scale” (Slonimsky’s term), Acoustic, and Overtone. Most of these names either reference other modes, specific literature, or operate on the well-established but completely erroneous notion that this mode is the most accurate 12-TET approximation of the lower partials of the overtone series. (The vast majority of publications–with the notable exception of Hindemith’s The Craft Of Musical Composition–get the 13th partial wrong. Assuming a fundamental of C, the 13th partial is about 41 cents sharp of A-flat, but 59 cents flat of the A-natural that forms a part of that scale. This is a bigger difference than the case of the 11th partial, where the necessary F-sharp is 48 cents flat.)
Thus, within my modal nomenclature, this mode is known by another name, which doesn’t tie its name to other modes, specific literature, or false premises about overtones: the Thracian mode, named after the ancient Greek region of Thrace.
How do you typically use these modes?
When I use the term “modal system”, some instinctively raise an eyebrow and launch into criticism of the use of “systems” in composition, and come to the conclusion that I am somehow more of a theorist than a composer as a result. While there are certainly some compositions in my oeuvre that one could point to as being “experiments” in acclimating myself to paradiatonic modal techniques, my use of them is not strict by any stretch—no more so than Beethoven’s use of the Ionian mode. I believe that extending my understanding and theory of what these modes mean in my music (and other’s music) is more important than shoehorning my music within a narrower, systematic definition (as Hindemith did with his infamous “revisions” to various pieces). Generally, as tradition goes, my theory of how the modes work in my music has lagged behind their actual application in my compositions, though as I am relatively observant of these tendencies, the lag between practice and theory is generally quite small. Over time, my particular modal sensibilities have become engrained, and simply pour out into anything I write, rather than starting from a more artificial point of specifically wanting to write something in G Andecavian, for instance. Often times, I will also tend to layer and mix modes and tonal centers to create polytonal and polymodal complexes.
Have others used these modes?
Yes, and for thousands of years. Prime examples include the South Indian raga system (there’s a lot in common between my system and the Melakarta ragas) and the music of Ancient Greece, and there are numerous examples elsewhere.
Outside world and ancient traditions, there are isolated examples up until the late 19th/early 20th century, when the use of expanded heptatonic modality exploded. Compelling examples can be found in works as well known as Debussy’s Nocturnes, Stravinsky’s Petrushka, and Holst’s The Planets.
How do things like octatonic scales and whole-tone scales fit into your modal system? Are they included?
By definition, a strictly heptatonic (7-tone) system excludes octatonic (8-tone) modes, including the popular “symmetrical” one (there are technically others). That said, there are ways to arrive at the same sound through polymodal means within a heptatonic approach. There are 14 modes in the system, belonging to two modal series, that form n-1 subsets of the octatonic scale, where one of the WH/HW segments is replaced with augmented second. Additionally, it can be arrived at by combining the lower tetrachords of two Dorian scales separated by a tritone, creating a “Bi-Dorian complex”.
Whole-tone scales are hexatonic (6-tone) modes. They are n-1 subsets of Set 3 of the heptatonic system, and omitting one note will yield a whole-tone scale. The addition of this “extra note” in a Set 3 mode (such as the Andrian mode, shown earlier) actually helps escape the peril of music quickly becoming monotonous, with all the intervals being the same size.
Are there microtones involved in the modal system? What kind of tuning is involved?
All of the modes in my catalog can exist within the standard 12-tone equal-tempered (12-TET) tuning system. However, my personal inclination in tuning actually bears some similarities to the approach of Aristoxenus in the fourth century BC. Rather than obsessing over precise ratios and “music of the spheres” concepts that the Pythagoreans espoused, Aristoxenus took a more practical and flexible approach to tuning, relying instead on ranges in which a given pitch could fall. At least to my ear, once an interval is exceedingly small (less than an eighth-tone, or 25 cents), the difference between the “correct” pitch and the actual pitch strikes me as a matter of timbre rather than pitch. In essence, it’s as if it is a different “flavor” of the same pitch. Sometimes, that timbral difference isn’t desirable, but other times, it works to good effect—-see the Von Karajan rendition of Holst’s “Mars” with the purposefully detuned horn section, or your average Balinese Gamelan for examples of this. It also can come about from natural tendencies when inflecting some of the more “characteristic” pitches and intervals of heptatonic modes, increasing their expressive capabilities.
If one were, for instance, to play a D Dorian scale in which the sixth-degree (B) ended up being an eighth-tone sharp, from this approach, it would still be considered a D Dorian scale, though the B would be “shaded” differently (to borrow from Ancient Greek terminology). It is essentially a “quantum effect” on the pitch–much like an electron in an atom, it can occupy a number of different positions in a “cloud”. (If it were to be played a quarter-tone flat, however, this would seem to pose a bit of a dilemma. It would be half-way between B and B-flat, and thus, halfway between being Dorian and Aeolian. The most logical way to consider this is as a microtonal Dorian-Aeolian “hybrid”, somewhere in between the two modes.
In essence, microtones are handled as “shades of gray”.
