The Locrian Mode: No, It’s Not Unusable
As a modal composer and theorist, known for geeking out about harmonic technique, I have always been fascinated by the way others perceive the Locrian mode. From my perspective, it is simply a mode, and one that I have been known to use on occasion in my own music—more frequently than Ionian, in fact. To others, however, it tends to be viewed with a sort of befuddlement, as the “black sheep” of the seven diatonic modes, due to the fact that its first and fifth scale degrees are a diminished fifth apart, instead of the perfect fifth contained in the other six modes in the series.
With perhaps the exception of the death metal community, it often tends to be treated as merely a theoretical curiosity for that reason. The oft-cited reason from common practice-inclined theorists is that Locrian’s “diminished tonic” is unstable and requires resolution, supposedly rendering the mode effectively unusable.
Locrian and its alleged “problem”
AUDIO: B Locrian Scale and Diminished Triad
This trope is oft-repeated in theory texts, method books, and general discussions of the (diatonic) modes. Some textbooks even try to pretend it doesn’t exist. People have been bagging on Locrian ever since Heinrich Glarean (who called it “Hyperaeolian”) rejected it from his expansion of the Renaissance-era modal system in his well-known 1547 treatise, Dodecachordon.
That reputation, however, is not deserved. Indeed, before the anonymous authors of the tenth-century treatise known as the Alia musica started applying the familiar Greek demonyms to the medieval catalog of diatonic modes, initiating our modern usage of them, the Greeks of centuries prior actually applied the names in a completely different order. In fact, in that system, the name “Mixolydian” did not refer to the mode we would typically think of today (i.e. G-A-B-C-D-E-F-G, and its transpositions), but what we now know as “Locrian”. (The modern use of the term “Locrian” to refer to B-C-D-E-F-G-A-B and its transpositions, per musicologist and mode scholar Harold Powers in The New Grove’s Dictionary of Music and Musicians, did not seem to come about until sometime after the eighteenth century.) It was not merely a “theoretical curiosity” to the ancient Greeks, either—we see evidence in the writings of Plato, Aristotle, and other philosophers suggesting active usage, with Aristoxenus (by way of Pseudo-Plutarch) crediting its invention to Sappho.
While there is one obvious way to enforce the tonal center in the Locrian mode—the “brute force” method, by using a drone (as is the typical death metal paradigm)—this approach is very unlikely to fully dismiss some of the skepticism directed at the mode, particularly with respect to its use in the context of larger progressions, and especially ones that can serve as an analogue to the tonal idea of “functionality”. This essay is my response to this challenge. While there are actually multiple ways of achieving success here, I will detail one particular approach, which provides a framework that is of considerable use in many other modal situations.
First off, I’ll remark on arguably the most biggest mistake that pretty much everyone in the “unusable” crowd makes: tertian bias. That’s a term I coined some time ago to refer to the fact that, outside the realm of post-tonal theory, there are still many that think strictly in terms of tertian (third-based) harmony, such as triads and seventh chords. Even jazz theorists resort to tertian-based kludges when confronted with the non-tertian harmonic constructs of the fusion sub-genre (the “sus”), due to the strong bias built into the ubiquitous lead sheet symbol system.
While my “modal advocacy” is fairly well-known, I am also an avid supporter of non-tertian harmony and its harmonic potential, particularly within the realm of modality. Indeed, once we remove the unspoken restriction of sticking to tertian harmony, the Locrian mode’s potential comes into focus. Taking such an approach allows us to completely circumvent that supposedly problematic “diminished tonic” by finding another harmonic entity to serve as a larger gestalt representation of the tonal center in the mode.
To hone in on what I mean by “non-tertian harmony”, I use the term to refer to any sort of harmonic structure that appears to be, wholly or in part, constructed of intervals other than thirds. The most commonly considered types of non-tertian harmony are quartal harmony (constructed of fourths), quintal harmony (constructed of fifths), and secundal harmony (constructed of seconds), but mixed and other structures are possible as well. The distinction between these types does start to break down once enough notes are accumulated—for instance, a chord consisting of all seven notes of a heptatonic mode could be considered a tertian thirteenth chord, but it could just as easily be stacked up all in fourths, as a secundal cluster, or any other combination of intervals, for that matter. The distinction between these types tends to make more sense when dealing with smaller chords, particularly in the range of three or four notes.
On the subject of stacking all seven notes of a heptatonic mode, Locrian becomes particularly interesting in this regard. If all the notes of the mode are stacked in fourths over the tonal center, the result consists entirely of perfect fourths. We will return to this thought shortly. (Interesting side note: its inverse, Lydian, can do the same thing with fifths.)
The result of stacking the Locrian mode in fourths, over its tonal center.
Now, it may be useful to get into a little bit of terminology, so we can get a little more of an idea of what we are doing within this expanded harmonic realm. My personal system I use for labeling harmonies in this environment is something I call “Arabic numeral analysis”. It bears some resemblance to the more familiar Roman numeral system, but strips out the tertian bias that permeates that system through and through.
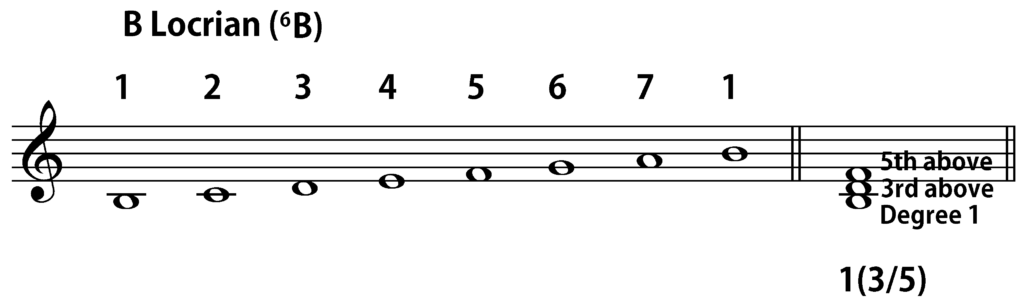
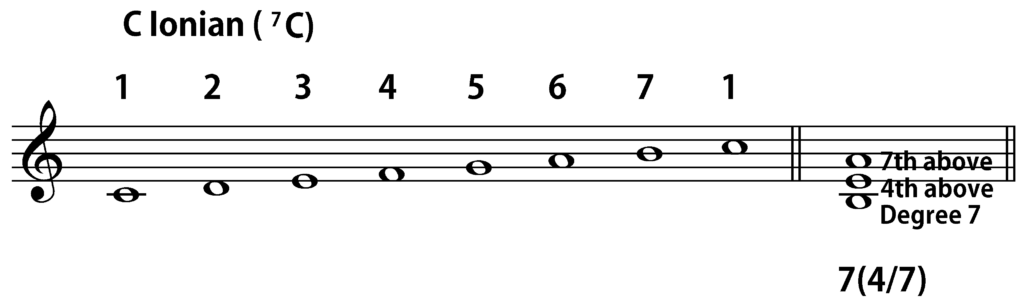
To give a brief overview of the system, let us first consider a very familiar harmony—a triad built on the tonal center. In Arabic numeral analysis, it would be symbolized as 1(3/5). The initial “1”, of course, indicates that the bass of the chord is scale degree 1 in the prevailing mode, while the “3/5” in parentheses shows that the upper notes of the chord form a third and a fifth (or some compound version of one or both intervals) above the bass. If we are using B Locrian (B-C-D-E-F-G-A-B) as a prevailing mode, 1(3/5) would be an indication that we are dealing with the chord B-D-F, or any voicing of those three pitches, where B is in the bass. (The 6B symbol is a shorthand for “Mode 6 on B”, as Locrian is the sixth mode in my Heptatonic Modal Catalog, since I begin the ordering with Dorian, not Ionian.)
1 (3/5) chord in B Locrian
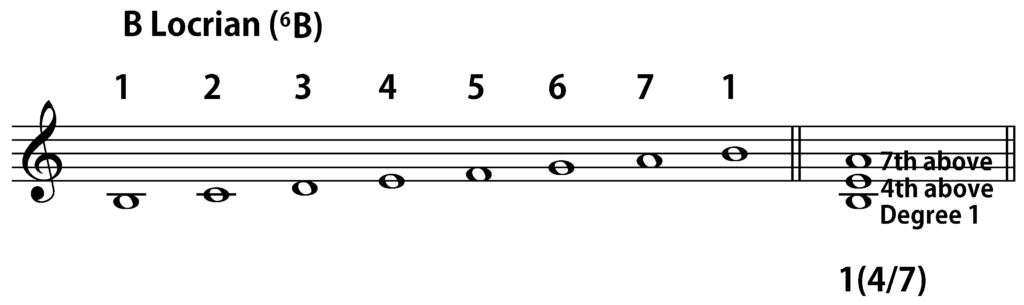
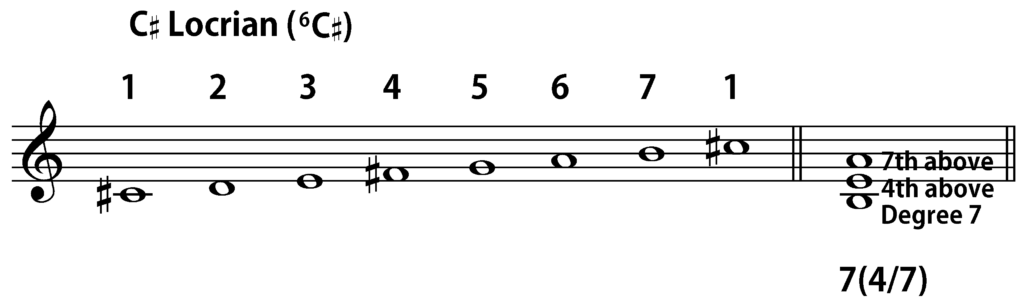
This approach immediately pays off when we start looking at non-tertian chords. Let us consider, for instance, the three-note quartal stack B-E-A. If we are in B Locrian, since B is scale degree 1, E is a fourth above B, and A is a seventh above B, the Arabic numeral symbol would be 1(4/7). If we were in C Ionian instead, since B would be scale degree 7 there, the chord would be 7(4/7) in that particular case. In E Dorian, it would be 5(4/7), and in C♯ Locrian, it is also a 7(4/7).
Analyses of the 4/7 chord B-E-A in several modal contexts.
Similarly, the mixed chord A-C♯-D, in the context of E Dorian, would be 4(3/4)—A would be scale degree 4, C♯ is a third above A, and D is a fourth above A.
4(3/4) chord in E Dorian – an example of a “mixed” harmonic species.
There are a number of other nuances to consider with this system in order to gain a full understanding of it (particularly with dealing with alterations, and the whole matter of how this system wreaks havoc on the common practice notion of chord inversions), but this information should be enough to process my demonstration below.
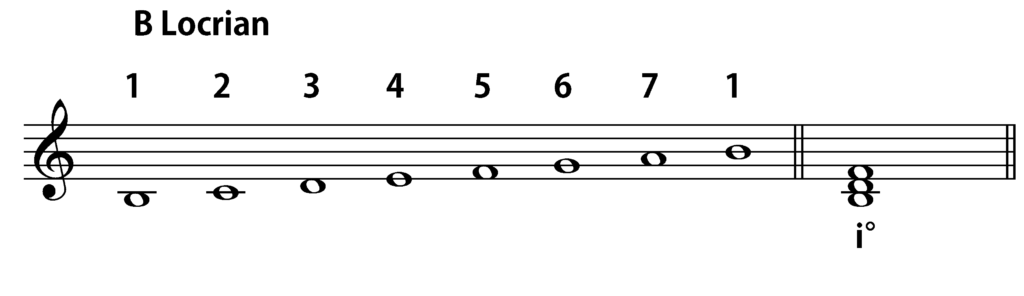
One other concept to consider is the placement of the other scale degrees in relation to the tonal center, which can play an important role in creating a sense of harmonic motion. To generalize this and strip out some of the common practice baggage, I use something called the “CPID model” (pronounced like “Cupid”). The “C”, in this case, refers to the central degree (degree 1). The “P” refers to “proximal” degrees, those adjacent to the center (degree 2 above and degree 7 below). The “D” to “distal” degrees, those farthest from the center (degrees 4 and 5), while the “I”, or “intermedial” degrees, lie in between (degrees 3 and 6). Each heptatonic mode will have a single central degree, and a pair each of proximal, intermedial, and distal degrees. Here is the CPID model on B Locrian:
CPID (“Cupid”) Model on B Locrian.
It is instructive to first take a look at the norms of common practice tonality through the CPID model. In cadential gestures that return back to a tonic (1) chord, we most often find the dominant (5) chord, which exists in a distal relationship against the tonal center. Occasionally, however, one may also encounter a leading-tone chord (7) used in a similar “dominant function” capacity, which would exist in a proximal relationship with the center. The next most common pre-resolution chord (“pre-dominant” in tonal terminology) in a common practice environment would be the subdominant (4) chord (in the case of the plagal cadence), which would also be distal to the center. From this, we can surmise that our tonal center is generally preceded by a chord built on a distal or proximal scale degree—go big or go (not far from) home. Going farther back to pre-dominant function chords in a common practice tonal environment, we find that those are also typically either proximal (ii/ii°) or distal (IV/iv).
Additionally, there is the matter of pitch inventory between the chords. In many cases in the common practice era, particularly when the chord before the tonic—the dominant function chord—has a seventh, the parent scale structure is actually completed or nearly completed between just it and the resolution chord. Counting the tones in both chords, the V7 resolution to I/i includes all notes in the scale except scale degree 6, and the vii°7/viiø7 resolutions include every note. This element of contrast also plays a role in the sense of harmonic motion.
Examples of “mode completion” in a stock common practice tonal context
We have already noted the fact that the Locrian mode produces a tritone-free stack of fourths, up through seven notes. This gives us a good starting point for how we might produce seemingly stable progressions in the mode, and avoid the aforementioned pitfalls that have prevented many from seeing the mode’s viability. Speaking as a modal composer, familiarizing oneself with the harmonic potential of an unfamiliar mode in a sort of “sandbox” setting—including its vast array of non-tertian resources—can be a very useful way to get one’s bearings. For myself, this acclimation has usually come from some combination of “theorizing on paper”, and actually playing around with that theorizing through improvisation, such that the sound and idea of the mode can start to be internalized. This becomes increasingly useful—and rapid—once one has an educated sense of what to expect from a given mode under different harmonic scenarios.
Taking into consideration the use of (a) non-tertian harmonies, (b) the CPID model, and (c) mode completion, it now becomes possible to look at some potential progressions in the Locrian mode, which actually create some form of modal analogue to functional tonality. For the sake of variety, I will be using C♯ Locrian (C♯-D-E-F♯-G-A-B-C♯) here, instead of B Locrian. (And for those who don’t yet realize it, all of the diatonic modes fit on the familiar circle of fifths, filling it with the equivalent of 84 “keys”, rather than a mere 24.)
Circle of fifths with all the diatonic modes (click to enlarge)
C♯ Locrian with CPID Labels
AUDIO: C♯ Locrian Scale
First off, let us begin with a four-note quartal stack for our chord on degree 1 (C♯), giving us C♯-F♯-B-E.
4-note Quartal Stack on C♯
AUDIO: 4-note Quartal Stack on C♯
By collapsing the tenth (C♯-E) down to its simple equivalent, the third, we end up with C♯-E-F♯-B:
Process of collapsing octave
End result
AUDIO: Collapsed 4-note Quartal Stack on C♯
In our Arabic numeral analysis system, using the most condensed method (in which compound intervals are collapsed down to their simple equivalents, and duplicates are ignored), both of these chords would be 1(3/4/7) chords. The latter, curiously enough, looks like a traditional seventh chord, in which the fifth has been swapped out for a fourth.
If we subtract the tones of this chord from our parent mode, the resultant negative space consists of scale degrees 2, 5, and 6. If we simply stack these in order, using scale degree 2 as the bass, the result is a 2(4/5). Again, this happens to bear some superficial resemblance to a triad, but with the third swapped out for a fourth. Having the fourth in place of the third goes a long way toward avoiding the previously mentioned pitfalls here as well.
Notes needed for mode completion shown with filled-in noteheads.
2(4/5) chord in C♯ Locrian, one realization of mode completion
The 2(4/5) chord is, of course, proximal to our tonal center, and at this point, it is worth checking the result of our initial groundwork. Progression 1 below is the result of using this 2(4/5) as a “dominant analogue”, sandwiching it between two 1(3/4/7) chords. (In case anyone is wondering what the bracketed “[Dor]” means, it is related to my concept of chord quality—it is not necessary to understand for the purpose of this demonstration, and is merely there for reference.)
AUDIO: Locrian Progression 1
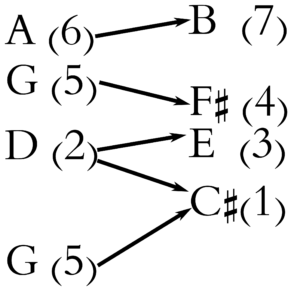
As you can see (and hear), the voice leading between these two chords is very smooth, and there should be some sensation from the listening example of the 1(3/4/7) chord, and its C♯ bass, seeming rather stable in this context.
Voice leading map on 2(4/5) – 1(3/4/7) in C-sharp Locrian (numbers in parentheses are scale degrees)
The feeling of centricity—or “tonic-ness”, for those coming from a tonal background—on the C♯ can be further amplified by using octave bass reinforcement, as Progression 2 demonstrates:
AUDIO: Locrian Progression 2
Bass reinforcement makes a fairly substantial difference in bringing focus and definition to this particular progression, namely due to the matter of bass clarity with the constituent intervals in the chords. That concept, due to its breadth, is best reserved for a future write-up. (In brief, my particular conception of intervals actually rejects the simple “consonance-dissonance” dichotomy for a two-dimensional interval characterization scheme, taking some inspiration from the work of Ernst Terhardt and Richard Parncutt.)
If we return to the CPID model, and the idea of chords with proximal and distal bass notes as potential dominant analogues, we have some other options to consider as well. Perhaps the most promising of these is by swapping out the proximal 2(4/5) for a distal 5(2/5) chord by changing the bass note from D to G, coupled with the bass reinforcement on the 1(3/4/7). Progression 3 examines this possibility.
AUDIO: Locrian Progression 3
Voice leading map for 5(2/5) to 1(3/4/7) resolution
Progressions 4 and 5 explore the alternate possibilities for proximal (7) and distal (4) motion, respectively, while also offering scale completion (albeit with tones in common with our 1(3/4/7) chord). The alternate distal option (Progression 5) has a dull, rough sound, in large part due to its inclusion of a displaced cluster (a compound second and third from the bass) and the presence of the sixth.
AUDIO: Locrian Progression 4
AUDIO: Locrian Progression 5
After evaluating these possibilities, I felt most drawn to extending Progression 3, with the 5(2/5) chord, into a larger progression that evokes an analogue to functionality. If we consider a rather common tonal progression—I-vi-ii-V-I—we find that under the CPID model, it produces the pattern C-I-P-D-C. Progression 6 also follows a C-I-P-D-C bass pattern, but in the Locrian mode and with non-tertian harmonies.
AUDIO: Locrian Progression 6
The use of the Locrian mode and non-tertian harmonies as in Progression 6 would be pretty far off the radar of conventional thinking, for a situation where “functionality” can exist. However, it should seem as if there is a strangely familiar sense about these progressions. That is, ultimately, the goal of an effort such as this one—to show one of many accessible ways of traveling into the (surprisingly) still open musical frontier of modal and non-tertian harmony.
Alexander LaFollett, Ph.D.
25 January 2018
UPDATE 13 Mar 2020: Hear the techniques described in this essay, in my Symphony No. 1 in C-sharp Locrian, Op. 58, 1st movement.
4 comments
3 pings
Skip to comment form
Hello Dr. LaFollett: Great article! I teach songwriting at Berklee, and for many years had what I thought was a fairly open-minded approach to turning songwriters on to the joys of modal writing, recommending fairly simple diatonic and, yes, tertian approaches for most of the modes. My narrative about Locrian, I confess, was pretty normative, and your article has made me re-think some of my biases in a really useful way. I especially like your insight about how the supposed unusability of Locrian, resting largely on the weakened tonic function of a diminished triad’s tritone on the root – reflects a strong dependence on tertial harmony. Hope to dig further into your work, both compositional and theoretical.
[ BTW: Your “octave completion” insight about the dominant seventh-tonic cadence, and then generalizing that, is very reminiscent of work done by Berklee guitar guru Mick Goodrick and Tim Miller on “generic modal compression.” ]
Most of what I read about the music modes other than Ionian (major) and Aeolian (minor) seems to take the position that the Locrian mode is the most mysterious, the most difficult to compose in, and generally to be avoided. Much is made of the fact, including reference to old myths about evil, that the fifth note in the Locrian scale is not a perfect fifth, but forms a tri-tone with the root. All the other six modal scales (Ionian, Dorian, Phrygian, Lydian, Mixolydian, and Aeolian) contain perfect fifths. Slight alterations to the Dorian, Phrygian, Lydian, and Mixolydian take them into the comfortable world of Ionian and Aeolian, our western music mainstays.
Well, that sounds too complacent and unimaginative and even risk-averse to me. We western composers are perhaps too fixated on major and minor keys. To some ears, even a minor key is upsetting, and a favorite practice is to switch to major at the end to lighten up the mood. What is the composer afraid of – that members of the audience will become clinically depressed? Or that they’ll throw rotten fruit at the performers? Or that they won’t buy the sheet music or CD?
Locrian mode can be made to sound beyond sad, but other treatments can make it sound surreal, otherworldly, and even mystical. The Icelandic pop star Björk had a hit Locrian tune, “Army of Me” (1995). In the movie “Dancer in the Dark” (2000), Björk used Locrian to portray an eerie sense of fun (dancing to machine noises) on the one hand, and a sense of sad resignation to her life without marriage, on the other.
Debussy, in “Jeux”, has a few passages in Locrian, which hardly sound sad, but more like playful fantasy.
To take the mystery out of composing in Locrian, we may treat it as we do a piece in a major or minor home key: The home key is the tonal center, but a piece doesn’t stay in the home key. A work in so-called “C major” spends time in F or G or E, maybe even A minor, or a transition using a diminished chord. But it “comes back to” or “is centered upon” C major as its home tonality.
Why not treat Locrian the same? Sure, the home chord is diminished, or if you use a four-note chord, it’s half-diminished. But the piece may travel to other tonalities involving major, minor, and other diminished chords. We can keep the Locrian diminished chord on the root note of the scale as the “home”, as unsettling as it may sound to our ears. And if you fear the audience, end it with a few bars of the corresponding minor or major key to give them the expected, the familiar.
To illustrate, here are suggestions for simple arrangements of “You Are my Sunshine” in B-major, then in B-minor, then in B-Locrian. The first uses notes b, c#, d#, and f# with chords B and F#. The second uses notes b, c#, d, and f# with chords Bmin and F# or F#min. The last uses notes b, c, d, and f with chords Bdim and F. Hear how the mood changes! The B-Locrian is moody, sad, surreal, sort of like being stuck at home – Bdim or Bm7(b5) – during the pandemic.
My illustration was for “Mary Had a Little Lamb”, I believe. “You Are my Sunshine” takes a few more notes and three chords instead of two, but the idea is the same.
Interesting. I had been wondering about the possibilities of constructing a form of para-functional harmony using modes, and it’s nice to see something systematic worked out.
[…] Minus some last edits, I’ve more or less finished my first symphony–legal name Symphony No. 1 in C-sharp Locrian, Op. 58. While I’ve written orchestral music before, writing a straight-up symphony has been a goal of mine since I started seriously composing in my teenage years (darn near two decades ago (!) at this point–wow, I’m old), and one at which I had many aborted attempts. (In fact, I was so superstitious about this past record that I referred to the piece as “The S-Word” until very late in the compositional process.) Recognizing the difficulty in getting a full orchestra work out into the world, and also the fact that I happen to play all the orchestral strings, I decided to go the string orchestra route, with the potential intent of pulling a Davide Rossi (kind of a hero of mine for working with The Verve–one of my all-time favorite bands) and just multi-tracking the whole thing myself, in order to get it out in the world. This past week, I happened to undertake my first step in that direction, by overdubbing myself 19 times (4x Violin I, 4x Violin II, 4x Viola, 4x Cello, 3x “Bass”–actually my infamous “detuned cello”, which you can hear here) and recording the coda section at the end of the first movement. The results of this quick trial recording can be heard below. And yes, that’s really the Locrian mode–the details of how I used it are pretty much exactly as described in my article, “The Locrian Mode: No, It’s Not Unusable”. […]
[…] yes, this thing is indeed in the Locrian mode–in fact, it spiraled out from my article “The Locrian Mode: No, It’s Not Unusable“, which goes into quite some detail about just what I ended up doing with this particular […]
[…] me and cataloged hundreds of other nonstandard modes; I’d encourage a read of his post titled The Locrian Mode: No, It’s Not Unusable. I might want to revisit his work later, as it seems thought-provoking. The man wrote a whole […]